1222. Queens That Can Attack the King

by

1222. Queens That Can Attack the King

Medium

On an 8×8 chessboard, there can be multiple Black Queens and one White King.

Given an array of integer coordinates queens that represents the positions of the Black Queens, and a pair of coordinates king that represent the position of the White King, return the coordinates of all the queens (in any order) that can attack the King.

Example 1:

img

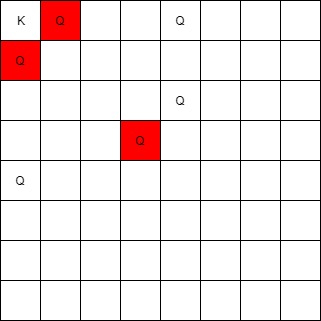
Input: queens = [[0,1],[1,0],[4,0],[0,4],[3,3],[2,4]], king = [0,0]
Output: [[0,1],[1,0],[3,3]]
Explanation:  
The queen at [0,1] can attack the king cause they're in the same row. 
The queen at [1,0] can attack the king cause they're in the same column. 
The queen at [3,3] can attack the king cause they're in the same diagnal. 
The queen at [0,4] can't attack the king cause it's blocked by the queen at [0,1]. 
The queen at [4,0] can't attack the king cause it's blocked by the queen at [1,0]. 
The queen at [2,4] can't attack the king cause it's not in the same row/column/diagnal as the king.

Example 2:

img

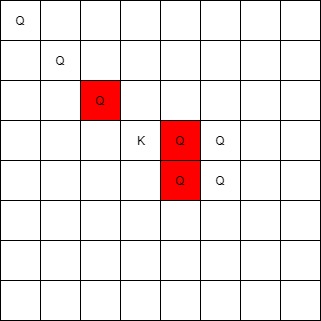
Input: queens = [[0,0],[1,1],[2,2],[3,4],[3,5],[4,4],[4,5]], king = [3,3]
Output: [[2,2],[3,4],[4,4]]

Example 3:

img

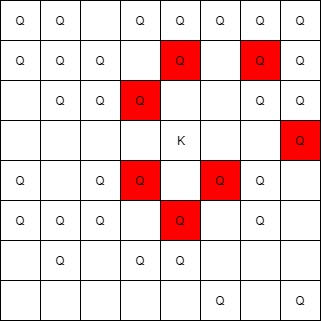
Input: queens = [[5,6],[7,7],[2,1],[0,7],[1,6],[5,1],[3,7],[0,3],[4,0],[1,2],[6,3],[5,0],[0,4],[2,2],[1,1],[6,4],[5,4],[0,0],[2,6],[4,5],[5,2],[1,4],[7,5],[2,3],[0,5],[4,2],[1,0],[2,7],[0,1],[4,6],[6,1],[0,6],[4,3],[1,7]], king = [3,4]
Output: [[2,3],[1,4],[1,6],[3,7],[4,3],[5,4],[4,5]]

Constraints:

  • 1 <= queens.length <= 63
  • queens[i].length == 2
  • 0 <= queens[i][j] < 8
  • king.length == 2
  • 0 <= king[0], king[1] < 8
  • At most one piece is allowed in a cell.

思路

King 最多受到来自 8 个方向的攻击（水平 2，垂直 2，对角 4）。因此开辟一个数组 queens_on_directions 用于存放每个方向上距离 King 最近的可发起攻击的 Queen。

遍历 queens 数组，对其中的每个 queen，首先判断其是否在 king 的八个可被攻击方向上（计算 queen 和 king 的横纵坐标差，并以 -1 表示不可攻击，0 – 7 表示 8 个可攻击方向）。

若可攻击，则判断当前的 queen 和之前此方向上的 queen 哪个距离 king 更近，并更新 queens_on_directions 数组。

遍历完 queens 数组后，返回 queens_on_directions 中的有效 queen。

int get_distance(vector<int> a, vector<int> b) {
    return abs(a[0] - b[0]) + abs(a[1] - b[1]);
}

int check_attackable(vector<int> queen, vector<int> tgt) {
    int horizontal = queen[0] - tgt[0];
    int vertical = queen[1] - tgt[1];
    
    if (horizontal == 0) return vertical < 0 ? 0 : 4;
    else if (vertical == 0) return horizontal < 0 ? 6 : 2;
    else {
        if (abs(horizontal) != abs(vertical)) return -1;
        else {
            if (horizontal < 0) {
                return vertical < 0 ? 7 : 5;
            }
            else {
                return vertical < 0 ? 1 : 3;
            }
        }
    }
}

class Solution {
public:
    vector<vector<int>> queensAttacktheKing(vector<vector<int>>& queens, vector<int>& king) {
        vector<int> null_queen = {-9, -9};
        vector<vector<int>> queens_on_directions(8, null_queen);
        for (auto queen: queens) {
            int attackable = check_attackable(queen, king);
            if (attackable == -1) {}
            else {
                int old_distance = get_distance(queens_on_directions[attackable], king);
                int new_distance = get_distance(queen, king);
                if (new_distance < old_distance) {
                    queens_on_directions[attackable] = queen;
                }
            }
        }
        
        vector<vector<int>> res;
        for (auto queen: queens_on_directions) {
            if (queen != null_queen) {
                res.emplace_back(queen);
            }
        }
        return res;
    }
};

Runtime: 4 ms, faster than 90.89% of C++ online submissions for Queens That Can Attack the King.

Memory Usage: 11.2 MB, less than 55.84% of C++ online submissions for Queens That Can Attack the King.

Leave a Comment